A system of equations
With the Board, Agent Set, Plant and Reporting subsystems defined, we now have a large system of concurrent nonlinear equations to solve
Summarising our core concept definitions and the agent priority model, and, for the example of LTI Plant and Reporting systems, we now have a large system of simultaneous equations describing the organisation’s dynamics across all ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() :
:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
In this model of the organisation, the Agent set will vary its priorities. Agents will allocate their time, on average, on tasks based on the evolution of the state of the plant and the reporting system, as well as the board plan. The Priority Tensor is the set of balancing endogenous variables that adjust in response to the board targets, plant and reporting system against the influence, judgement and incentive tensor of the Agent set.
The organisation thus adapts its priorities over time based on these characteristic tensors and their interplay with the Board targets and the dynamics of the plant and reporting systems.
Our initial system diagram can now be updated with key signal flows based on our system of equations in Exhibit 1.
Exhibit 1:
Framework model components and with signal flows
Source:
Aethon
Solving the system equations
We use the following iterative process to estimate the evolution of the system state over time. The code is available in the Tools section of this website
The set of differential equations in (4) does not have a straightforward closed-form solution. Under this model, calculating the evolution of the system state, including the priority, plant state and reporting tensors, is a numerical problem. Furthermore, the stochastic nature of Agent state transitions means that any such solution requires Monte Carlo simulation methods in discrete time, using a clock tick of ![]() representing the interval of regular Agent state transitions..
representing the interval of regular Agent state transitions..
We have built a general case of this simulation model on Node.js and have made it available in the Tools section of this website under an MIT license. We use the following iterative process to estimate the evolution of the system state over time.
- Initialise all variables, setting
- The initial priority matrix
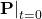
- The initial plant state
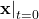
- The initial reporting vector
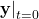
- The board targets
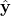
- The plant operating safe state
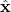
- The initial priority matrix
- Establish the state of all Agents
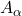 based on
based on 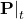
- Calculate the control input tensor
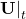
- Over a small time interval
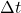 , estimate:
, estimate:
- The change in plant state
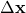 using the equations for the plant dynamics model and calculate the new state
using the equations for the plant dynamics model and calculate the new state 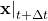
- The change in reporting
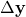 using the equations for the plant dynamics model and calculate the new state
using the equations for the plant dynamics model and calculate the new state 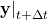
- The new priority tensor
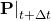 using equation (4)
using equation (4)
- The change in plant state
- Return to step 2 until the end of the simulation time period
The core classes of the model are abstract enough to be leveraged for modelling different Workstation, Plant and Reporting systems and behaviours.
System behaviour
The behaviour of individual systems will depend greatly on the scale, in terms of headcount, and specific configuration of the influence, judgment and incentive tensors, as well as the nature of the plant and reporting systems. Nevertheless, we can glean useful insights from simple model cases thereof.
The type of system outlined above is complex, nonlinear, and can demonstrates a very broad range of dynamic behaviours depending on its configuration. Even for a simple LTI Plant and Reporting system, there is a very large number of exogenous variables at play. This would be consistent with the real-life, empirical qualitative observation that organisations tend to be incredibly diverse, arguably demonstrating more differences between each other than e.g. humans do.
For real-world systems, these variables are practically impossible to measure in completeness, and the solution to the system of equations may not even be computable, in the the Turing sense. However, we can glean significant insights for real-life problems by simulating and studying the behaviour of simple systems.
We next proceed to describe the findings using such a simple model of a consensus-based organisation that we call C1.