The state space model
We use a very standard mathematical construct called a state space to describe organisations as dynamic systems.
We view organisations as dynamic, non-linear systems and describe them using a generic state space model. This work deals with tensors of unspecified size, extensible to Hilbert spaces, and uses Einstein notation where appropriate.
System components
An organisation is an interconnected system of people, physical assets and a reporting system built to solve a problem on behalf of a Board.
We define an organisation as the combination of a group of people and a set of physical assets as a system aimed at solving a problem: building, selling and supporting software, producing an affordable ketchup sauce, developing real estate projects or running a country’s healthcare system.
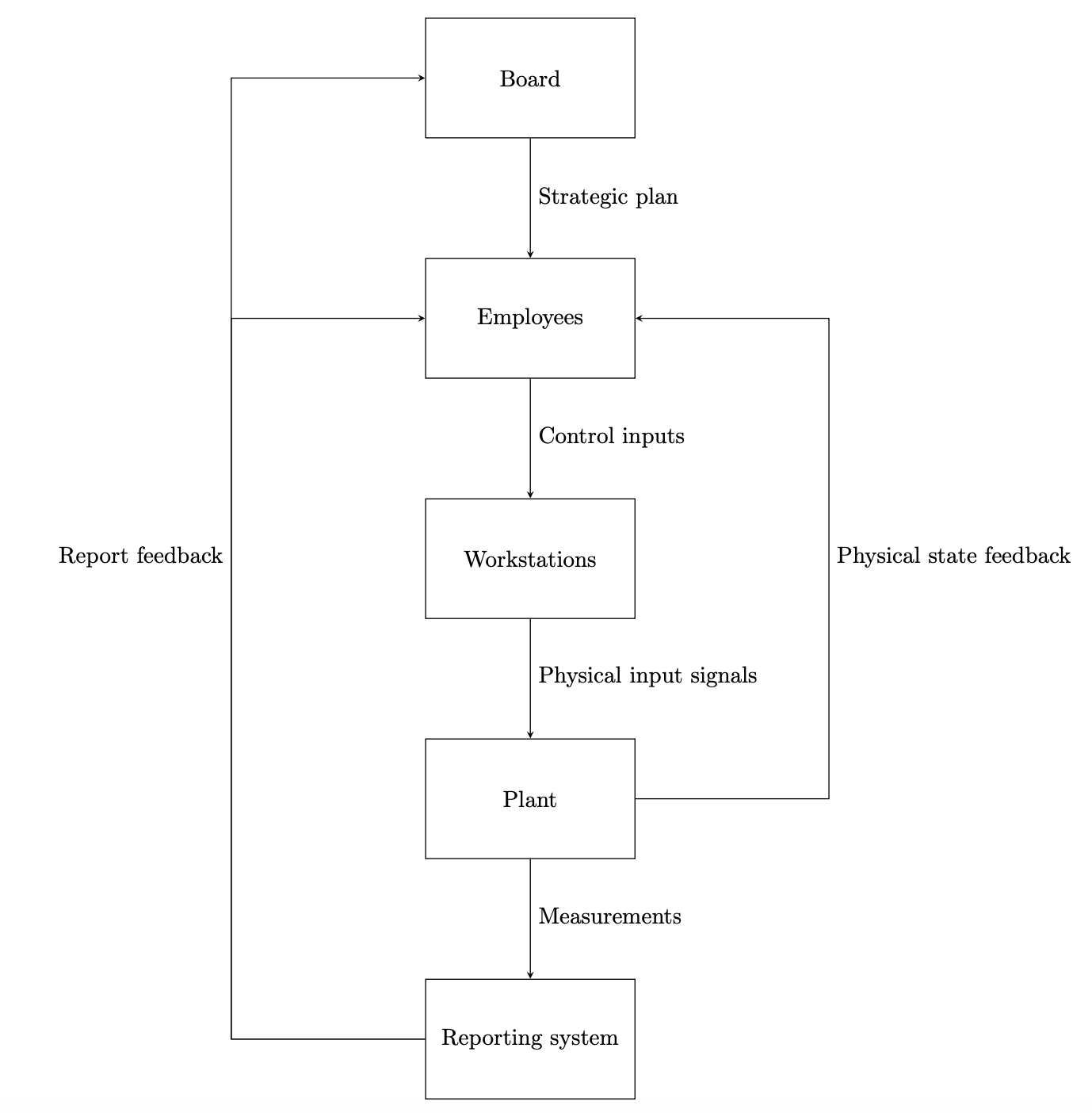
We model the organisation as a dynamic system with five main block components, or domains of objects, as shown in Exhibit 1 and, simplified, in Exhibit 2.
Exhibit 1:
Framework model components
Source:
Aethon
- The Board sets strategic priorities and financial targets.
- These priorities are communicated to the organisation’s members or employees, which we call Agents.
- The Agents attempt to execute on these priorities by performing physical activities, whether equipment control or physical labour, at their Workstations.
- The Plant, that is, the organisation’s property plant and equipment or the system of physical assets under the control of Agents, responds to control signals from employees.
- Finally, a Reporing System provides the Board and Agents with measurements of key performance indicators, including, but not limited to, financial accounting metrics.
Exhibit 2:
Framework model components, simplified
Source:
Aethon
Agents
Agents perform different tasks in discrete time with random probabilities, determined by their context/ state.
Let the organisation be the system emerging from the actions of a set ![]() of independent employees, which for the sake of generality we refer to as agents,
of independent employees, which for the sake of generality we refer to as agents, ![]()
![]()
![]() . We denote the number of agents as
. We denote the number of agents as ![]() , the cardinality of
, the cardinality of ![]() .
.
We model the behaviour of each ![]() as a finite state automaton. At any discrete time tick
as a finite state automaton. At any discrete time tick ![]() , each of
, each of ![]() transitions between a discrete set of states
transitions between a discrete set of states ![]() . At each moment in time, each
. At each moment in time, each ![]() is in one state
is in one state ![]() . Each
. Each ![]() represents
represents ![]() performing a single, atomic task, that is, the allocation of time towards a specific activity. The number of potential states of each agent is
performing a single, atomic task, that is, the allocation of time towards a specific activity. The number of potential states of each agent is ![]() .
.
With ![]() being a stochastic finite state automaton, the probability
being a stochastic finite state automaton, the probability ![]() of being in an arbitrary state
of being in an arbitrary state ![]() at time
at time ![]() , is given by:
, is given by:
(1) 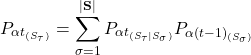
Where ![]() is the likelihood of state transition from
is the likelihood of state transition from ![]() to
to ![]() at time
at time ![]() , and
, and ![]() is the probability of
is the probability of ![]() being in state
being in state ![]() at time
at time ![]() .
.
Workstations
Workstations are an abstraction of the human interfaces between our priority-setting cognition and the real world of action.
Each agent operates a workstation.
Workstations model the human interfaces of physical equipment, whether the controls of a piece of machinery such as a sheet press, the keyboard and mouse of a computer or the keys of a musical instrument, or other physical object that constitutes the ![]() ‘s interface to the totality of the organisation’s property, plant and equipment.
‘s interface to the totality of the organisation’s property, plant and equipment.
We define a control input vector space with ![]() orthogonal unit basis vectors
orthogonal unit basis vectors ![]() , each of which represents a different type of input signal that an agent can send to the plant system.
, each of which represents a different type of input signal that an agent can send to the plant system.
Each agent ![]() in state
in state ![]() then emits a workstation control input vector
then emits a workstation control input vector ![]() in the control input vector space, based on a workstation function
in the control input vector space, based on a workstation function ![]() :
:
(2) ![]()
Thus at any time ![]() , each agent
, each agent ![]() emits a workstation control input vector
emits a workstation control input vector ![]() based on their state. The tilde symbol in
based on their state. The tilde symbol in ![]() indicates that the vector is stochastic, based on each Agent’s priority matrix, and captures
indicates that the vector is stochastic, based on each Agent’s priority matrix, and captures ![]() ‘s control signals to the organisation’s Plant system.
‘s control signals to the organisation’s Plant system.
Overall, at any time, the full agent set ![]() emits a control input tensor
emits a control input tensor ![]() , of rank 2, as an input into the Plant system, with elements
, of rank 2, as an input into the Plant system, with elements ![]() where
where ![]() .
.
The Plant
The organisation’s Plant is its collection of physical, real-world assets
The Plant model captures the physical dynamics of the organisation’s property, plant and equipment. This can be any type of physical production system, whether a blast furnance, an assembly line, a power station fleet, a manufacturing supply chain system, a restaurant network or an IT system on which code is built, tested and deployed.
Such a system may have inherent nonlinearities. Processes may be parallel or serial and may be subject to logical OR or AND conditions, based on task interdependencies; for example, the completion of a task or output may require the contribution of two Agents via their Workstations, such as two developers having to complete work on two separate modules of code for a feature to ship. There may also be time lags involved, for example the time between the seeding and harvest for a farm.
For a simplified linear time invariant (LTI) operating system plant with state vector x, and in line with standard state space model notation, the dynamics would be governed by a differential equation of the form:
(3) 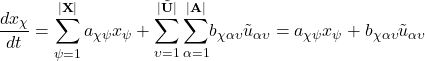
![]() is an element of the system’s state vector
is an element of the system’s state vector ![]() , and
, and ![]() is the number of degree of state space variables of the plant.
is the number of degree of state space variables of the plant.
We also define a plant target state vector ![]() , with elements
, with elements ![]() , representing the desired optimal or safe state of which the plant should be run at any time.
, representing the desired optimal or safe state of which the plant should be run at any time.
The Reporting System
The reporting system represents the organisation’s accounting system. It’s the information flows that measure and present performance, financial or otherwise. It closes the information feedback loop between agent and plant actions and outcomes, as measured.
Ultimately, the Board and Agents, including management, view a set of reported performance metrics or KPIs available to them.
The reporting system models the accounting systems used to produce these reports, including the organisation’s profit and loss, balance sheet and cashflow statement accounts.
In addition to the Plant, there might be inherent nonlinearities in the reporting system. For a simple, standard linear state space model, each observed ouput out of a total of ![]() from our system,
from our system, ![]() , can be written as:
, can be written as:
(4) 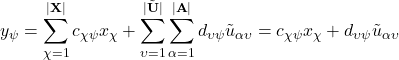
Where ![]() is an element of the report vector
is an element of the report vector ![]() holding all the reported output metrics.
holding all the reported output metrics.
The Board
The Board reviews performance and sets targets at regular intervals. The targets are fed into the Agent set as inputs of what the shareholders expect the organisation to achieve.
The Board establishes the system’s targets, in terms of a reporting (profit and loss, balance sheet, return on equity and so on) target. This is equivalent to a control signal into the agent set, in other words, the instructions to the employees.
We define the strategic plan vector ![]() , with elements
, with elements ![]() , where
, where ![]() , as the Board input to the Agent set providing the main control signal from the Board into the organisation.
, as the Board input to the Agent set providing the main control signal from the Board into the organisation.